2. DETERMINACIÓN O DEFINICIÓN DE UN CONJUNTO
2.1. POR EXTENSIÓN Y COMPRENSIÓN
Un conjunto queda perfectamente definido si se conocen con
exactitud los elementos que lo integran o que pertenecen a él; es decir, si se
nombran todos sus elementos o bien si se usa un enunciado o propiedad que lo
identifique. Independientemente de la forma en que se lo represente, siempre se
usa una letra mayúscula que lo define. Esta letra mayúscula
representa a un conjunto específico de elementos.
Existen dos maneras de definir un conjunto
dado:
2.1.1.Por extensión o enumeración: se
define nombrando a cada elemento del conjunto.
2.1.2.Por comprensión: se define mediante
un enunciado o atributo que representa al conjunto (se busca una frase que
represente a la totalidad de elementos sin nombrar a ninguno en particular).
Haz clic para ver vídeo
Por comprensión
|
Por extensión
|
A = {Números dígitos}
|
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
|
B = {Números pares]
|
B = {2, 4, 6, 8, 10, 12, 14, ...}
|
C = {Múltiplos de 5}
|
C = {5, 10, 15, 20, 25, 30, 35...}
|
2.2. RELACION ENTRE CONJUNTOS
SUBCONJUNTO
SUBCONJUNTO
Para representar que un conjunto es subconjunto de otro usamos este símbolo que tiene la forma de una U acostada y subrayada.
Sean los conjuntos A={ 2,4,6,8,} y B={ 0,1, 2, 3,4, 5,6,7,8.9 }
En este caso decimos que A esta contenido en B, o que A es subconjunto de B. En general si A y B son dos conjuntos cualesquiera, decimos que A es un subconjunto de B si todo elemento de A lo es de B también.
Existen dos tipos de conjuntos:
2.3.1. Conjunto Disyunto.
Son aquellos conjuntos que no tienen elementos en común.
ejemplo:
El conjunto A tiene como elementos a los números 1, 2 y 3.
El conjunto B tiene como elementos a las letras a, b, c y d.
No hay elementos comunes entre los conjuntos A y B.
En otras palabras, ningún elemento del conjunto A pertenece al conjunto B; a su vez, ningún elemento de B pertenece al conjunto A.
El conjunto B tiene como elementos a las letras a, b, c y d.
No hay elementos comunes entre los conjuntos A y B.
En otras palabras, ningún elemento del conjunto A pertenece al conjunto B; a su vez, ningún elemento de B pertenece al conjunto A.
En consecuencia, los conjuntos A y B son disjuntos.
2.3.2. Conjunto subconjunto
Un conjunto es subconjunto de otro si todos los elementos de un conjunto también pertenecen al otro.
Si se tienen los siguientes conjuntos:
P = {a, e, i, o, u} y R = {a, i}
R es subconjunto de P porque todos los elementos de R están en P.
En general, para expresar que un conjunto es subconjunto de otro conjunto se pone entre ellos el símbolo  . En este ejemplo se escribe:
. En este ejemplo se escribe:
 . En este ejemplo se escribe:
. En este ejemplo se escribe:
R  P
P
Se lee “R es subconjunto de P”
No es subconjunto de otro cuando al menos un elemento del primero no pertenece al segundo conjunto. El símbolo que representa la frase “no es subconjunto de“es  .
.
 .
.
Si se tienen los siguientes conjuntos:
C = {3, 5, 7, 9} y H = {3, 5, 8}
H no es subconjunto de C porque el elemento 8 no pertenece al conjunto C. Se escribe:
H  C
C
Se lee “H no es subconjunto de C”
También los subconjuntos pueden representarse mediante Diagramas de Venn.
Ejemplo:
2.4. CLASES DE CONJUNTOS
Según el número de elementos que conforman un conjunto, éstos se clasifican en:
2.4.1.Universal o referencia
2.4.2.Vacío.
2.4.3.Unitario.
2.4.4.Finito.
2.4.5.Infinito.
El conjunto universal o referencia, es el formado por un amplio número de elementos, como puede ser el conjunto de los números naturales o por letras del abecedario. Estos conjuntos sirven de base para crear más conjuntos.
Para representar que un conjunto es universal se utiliza la vocal U mayúscula.
Ejemplo:
El conjunto formado por las letras del abecedario.
U = {letras del abecedario}
El conjunto vacío es el conjunto que no contiene ningún elemento. Puesto que lo único que define a un conjunto son sus elementos, el conjunto vacío es único.
El conjunto vacío tiene las siguientes propiedades generales:
|
Muchas afirmaciones sobre el conjunto vacío son trivialmente ciertas, debido a la siguiente propiedad:
|
Este teorema es cierto porque el conjunto vacío no tiene elementos, y decir "todo hombre en Ø; es inmortal" es lo mismo que afirmar que "no hay ningún hombre mortal en Ø", y esto último es trivialmente cierto.
|
2.4.3. Conjunto unitario
En la teoría de conjuntos se define como conjunto unitario a aquel que está formado por un solo elemento.
Ejemplo:
A = { x } El conjunto A tiene un solo elemento que es: x
2.4.4.Conjunto finito:
Si al contar el numero de elementos que tiene el conjunto el conteo termina, se dice que el conjunto es finito.
Ejemplo: M = {x / x es un río de la tierra} Conjunto finito
2.4.5. Conjunto infinito: Si al contar el numero de elementos que tiene el conjunto el conteo no termina, se dice que el conjunto es infinito.
Ejemplo: A= {Las estrellas del universo}
N = {0, 1, 2, 3, 4, 5, 6, 7, 8,...} Conjunto infinito
V = {3, 6, 9, 12, 15, 18, 21, ,...} Conjunto infinito
V = {3, 6, 9, 12, 15, 18, 21, ,...} Conjunto infinito
ACTIVIDAD 3
"DETERMINACIÓN DE CONJUNTOS Y RELACIÓN ENTRE CONJUNTOS"
Formulario para evaluar conocimientos adquiridos sobre el tema
Nota: Recuerde que todos los campos son obligatorios
CLIC EN ACTIVIDAD 4. "CLASES DE CONJUNTOS"
CLIC EN ACTIVIDAD 5. CRUCIGRAMA
REFERENTES CONCEPTUALES
http://www.ejemplode.com/5-matematicas/2732-ejemplo_de_conjunto_unitario.html
http://misdeberes.es/tarea/39605
http://www.gcfaprendelibre.org/matematicas/curso/los_conjuntos









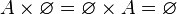



No hay comentarios:
Publicar un comentario